Saturated Model and Non positive - OSMASEM
 angelprieto
Joined: 03/16/2021
angelprieto
Joined: 03/16/2021
| Attachment | Size |
|---|---|
| Sin título.png | 13.71 KB |
| converged.dat | 542 bytes |
| non-converged.dat | 547 bytes |
Dear Cheung,
First of all, thank you for your helpful and inspiring contribution. We are very grateful for your interesting work and now we are trying to follow your steps and conduct a meta-analysis. However, on the way, we have had some doubts that we wanted to share with you as we are looking for some advice.
We conducted a data collection of the correlations between an income and longitudinal outcome. Let's imagine, resilence as income and anxiety as outcome. That is, we collected three correlations per study and the time elapsed between waves. When we calculated the degrees of freedom (DF) of the model, we supposed that elapsed time would increase the DF.
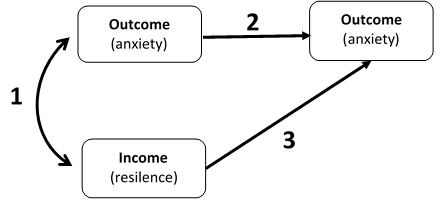
We run the model using the code displayed below and we found convergence in some cases (some combinations of incomes/outcomes/population), while in other cases unfortunately the model failed to converge even using rerun(). Additionally, we realized that our model had not enough degrees of freedom to estimate the fit indices.
Our doubts are the following:
- Apart from rerun() function, is there any way or method to get convergence in OSMASEM?
- have you got any recommendation for cases in which there are not enough degrees of freedom to estimate fit indices? Is it a usual practice to publish the results without fit indices in this type of methodologies? In connection with this, have you got any idea on how to deal with the lack of fit indices when reporting data in a paper?
Thank you very much in advance,
best regards.
NOTE: I attach a data frame with convergence (converged.dat) and without convergence (non-converged.dat). Both document are .RData (not allowed by this forum). But I have saved as .dat.
The code:
load("non-converged.dat")
#load("converged.dat")
data <- datos$data
n <- datos$n$N2
lag<-datos$lag$Tiempo
my.df <- Cor2DataFrame(data, n, acov = "weighted")
my.df$data <- data.frame(my.df$data, Lag=scale(lag),
check.names=FALSE)
pattern.na(my.df, show.na=FALSE, type="osmasem")
model1 <- 'O2 ~ o1o2*O1 + i102*I1
I1 ~~ i1WITHo1*O1
I1 ~~ 1*I1
O1 ~~ 1*O1
O2 ~~ Errs2*O2'
RAM1 <- lavaan2RAM(model1, obs.variables=c("O1", "I1", "O2"))
Ax <- matrix(c(0,0,0,
0,0,0,
"0*data.Lag","0*data.Lag",0),
nrow=3, ncol=3, byrow=TRUE)
fit<-osmasem(model.name="Ax as moderator",RAM=RAM1,Ax=Ax, data=my.df)
fitSum<-summary(fit,fitIndices=TRUE)
fit<-rerun(fit, autofixtau2=TRUE)
fitSum<-summary(fit)
fitSum
The output:
free parameters:
name matrix row col Estimate Std.Error A z value Pr(>|z|)
1 o1o2 A0 O2 O1 0.72942797 61.868395 0.0117899935 0.9905932
2 i102 A0 O2 I1 0.08720208 67.308102 0.0012955659 0.9989663
3 i1WITHo1 S0 I1 O1 -0.24744425 50.713200 -0.0048792868 0.9961069
4 o1o2_1 A1 O2 O1 0.03189127 56.278375 0.0005666701 0.9995479
5 i102_1 A1 O2 I1 -0.06617169 60.655999 -0.0010909340 0.9991296
6 Tau1_1 vecTau1 1 1 -22.14979597 NA ! NA NA
7 Tau1_2 vecTau1 2 1 -3.07424264 3.032155 -1.0138804284 0.3106398
8 Tau1_3 vecTau1 3 1 -84.96040254 NA ! NA NA
Model Statistics:
| Parameters | Degrees of Freedom | Fit (-2lnL units)
Model: 8 10 -32.15276
Saturated: 9 9 NA
Independence: 6 12 NA
Number of observations/statistics: 556/18
Information Criteria:
| df Penalty | Parameters Penalty | Sample-Size Adjusted
AIC: -52.15276 -16.15276 -15.889510
BIC: -95.36045 18.41338 -6.982323
To get additional fit indices, see help(mxRefModels)
timestamp: 2021-03-25 17:06:22
Wall clock time: 0.1089311 secs
OpenMx version number: 2.17.4
Need help? See help(mxSummary)
There are only 7 or 8 studies
There are only 7 or 8 studies per correlation. It is hard to defend a "typical" meta-analysis with 7 studies. In your example, it is even more difficult to justify it in OSMASEM, which is a multivariate analysis.
> pattern.na(my.df, show.na=FALSE, type="osmasem")
Mind_Out1 Out2_Out1 Out2_Mind
Mind_Out1 7 7 8
Out2_Out1 7 7 8
Out2_Mind 8 8 8
Log in or register to post comments
In reply to There are only 7 or 8 studies by Mike Cheung
Thank you very much for your
Thank you very much for your quick answer. We have other combinations with 14 studies (13-14 studies per correlation) or 25 studies (23-25 studies per correlation). In your opinion, which would be the minimum number of studies required to conduct a typical "meta-analysis" using TSSEM? and to conduct OSMASEM?
In these cases in which we have from 14 to 25 studies, we still are not sure of how to deal with the lack of fit indexes. Would you have any recommendations?
Thank you very much in advance,
Log in or register to post comments
It is hard to give a minimum
It is hard to give a minimum no. of studies as it depends on many factors. But 23-25 studies per correlation seems to be okay.
The function does not report any fit indexes when there are moderators. It is because it is not clear how to calculate these fit indexes in the presence of moderators.
Log in or register to post comments
Dear Cheung,
Dear Cheung,
Thank you once again for your quick and attentive response.
As we have mentioned in this thread our model has not enough degrees of freedom to estimated fit indices, therefore it is saturated. Considering this limitation, we think that running a path analysis based on OSMASEM or TSSEM is maybe not a good idea. We are considering the possibility of obtaining the pooled correlation matrix using the first step of TSSEM. Then, as the second step, we would conduct a simple linear regression based on the pooled correlation matrix. Do you think this methodology would make sense? Have you got any further considerations?
Thank you in advance,
Log in or register to post comments
Whether it is a path model or
Whether it is a path model or regression model depends on your research questions. I do not see any issue here.
Log in or register to post comments