Looking for help with including a moderator to a path model

In sort of new to SEM / modelling in general. So far I managed to make some sense of lavaan() syntax in R, to run a path model like this (file attached).

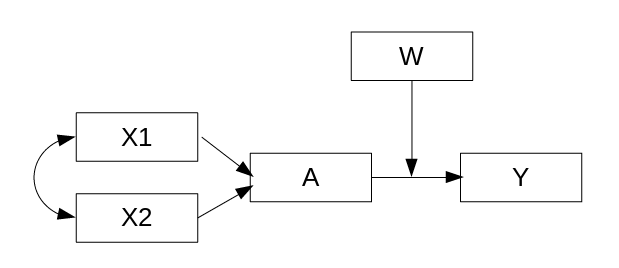
Before introducing the W moderator (continuous) this model was specified (in lavaan) as:

model <- '
X1 ~~ X2
A ~ X1 + X2
Y ~ A'


All variables are observed and continuous.

Now I'm trying to include the moderating effect of W on the effect of A on Y.

I have no clue on how to do it technically - syntax wise, and how to extract all of this from lavaan output for interpretation.

What I'm interested in is: whether or not W serves as a valid moderator and if yes how does it moderate the effect of A on Y.

Could anyone please give me a helpful hand?

I have openMX installed in my RStudio and don't mind switching to it - for now, as a beginner I found lavaan's syntax easier to understand.