CSOLNP Documentation¶

CSOLNP is an open-source optimizer engine for the OpenMx package. It is a C++ translation of solnp function from the Rsolnp package, available on CRAN. The algorithm solves nonlinear programming problems in general form of:

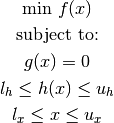
$\begin{eqnarray*} &\text{min } f(x) \\ &\text{subject to:}\\ & g(x) = 0\\ & l_{h}\leq h(x)\leq u_{h}\\ & l_{x}\leq x \leq u_{x}\\ \end{eqnarray*}$

Where:
 : Vector of decision variables ().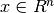
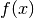 : Objective function ().
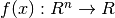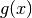 : Equality constraint function ().
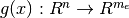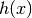 : Inequality constraint function ().
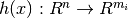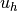, : Lower and upper bounds for Inequality constraints.
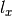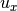, : Lower and upper bounds for decision variables.

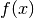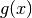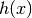$f(x)$ , $g(x)$ and $h(x)$ are all smooth functions.

Each major iteration of the optimization algorithm solves an augmented Lagrange multiplier method in the form of:

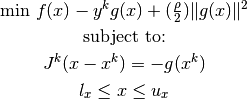
$\begin{eqnarray*} &\text{min } f(x)- y^k g(x)+(\frac{\rho}{2}) \lVert {g(x)} \rVert^2\\ &\text{subject to:}\\ &J^k (x-x^k )= -g(x^k )\\ &l_{x}\leq x \leq u_{x}\\ \end{eqnarray*}$

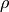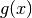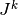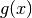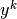Where $\rho$ is the penalty parameter. $g(x)$ denotes all the constraints including equality constraints and inequality constraints, which are converted to equalities by adding slack variables. $J^k$ is the Jacobian of first derivatives of $g(x)$ , and $y^k$ is the vector of Lagrange multipliers. The superscript 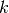$k$ denotes the 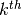$k^{th}$ major iteration.

Each major iteration starts with a feasibility check of the decision variables $x^k$ , and continues by implementing a Sequential Quadratic Programming (SQP) method, which calculates the gradient and the Hessian for the augmented Lagrange multiplier method. The criteria for moving to the next major iteration is satisfied when a Quadratic Programming problem of the form:

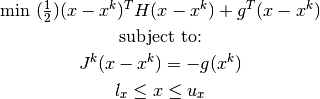
$\begin{eqnarray*} &\text{min } (\frac{1}{2}) (x-x^k )^T H(x-x^k )+g^T (x-x^k)\\ &\text{subject to:}\\ &J^k (x-x^k )= -g(x^k )\\ &l_{x}\leq x \leq u_{x}\\ \end{eqnarray*}$

results in a feasible and optimal solution to the augmented Lagrange multiplier problem. If the solution is not feasible or optimal, a new QP problem is called (minor iteration) for updating the gradient and the Hessian. The stop criterion for the optimization is either when the optimal solution is found, or when the maximum number of iterations is reached.

Input¶

Before providing an explanation of each input for CSOLNP, it is necessary to look at the “Matrix” structure defined for the use of any vector or matrix needed throughout CSOLNP.
“Matrix” is a structure containing three fields being:
int rows: Number of rows of the matrix.
int cols: Number of columns of the matrix.
double *t: Pointer to an array of doubles storing the matrix elements.

The arguments are:
- solPars: A Matrix of starting values for decision variables.
- solFun: Pointer to the objective function which takes the decision variable Matrix as input and returns the objective value.
- solEqB: A Matrix of equality constraints.
- solEqFun: Pointer to the equality constraint function which takes the decision variable Matrix as its argument, and returns a Matrix of evaluated constraints.
- solIneqFun: Pointer to the inequality constraint function with the Matrix of decision variables as input, and a Matrix of evaluated inequality constraints as output.
- solIneqLB: Matrix of lower bounds for inequality constraints.
- solIneqUB: Matrix of upper bounds for inequality constraints.
- solLB: Matrix of lower bounds for decision variables.
- solUB: Matrix of upper bounds for decision variables.
- solctrl: Matrix of control parameters containing:
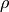: The penalty parameter in the augmented objective function with the default value of 1.
maxit: Number of major iterations with the default value of 400.
minit: Number of minor iterations with the default value of 800.
: Step size in numerical gradient calculation with the default value of 1e-7.
tol:  Relative tolerance on feasibility and tolerance with the default value of 1e-8.
- verbose: An integer variable with 3 levels (1, 2, 3) for printing throughout CSOLNP. verbose = 3 prints every calculation within CSOLNP.

Output¶

A structure containing the following values:
- Final objective value.
- Optimal estimations of decision variables.
- Hessian at the optimal solution.
- Gradient at the optimal solution.
- A variable named inform reporting the result of the optimization (same as inform variable returned by NPSOL optimizer). The following scenarios are reported by different values of inform:
inform = 0: Optimal solution is found.
inform = 1: The optimal solution is found but not to the requested accuracy.
inform = 4: Maximum number of major iterations is reached.
inform = 6: No improvement can be made to the current point (no convergence).

Example¶

To be provided

Restoring NPSOL¶

To use NPSOL, your OpenMx must be compiled to include it. If NPSOL is available, you can make it the default optimizer with

mxOption(NULL, “Default optimizer”, “NPSOL”)

You can also control this setting with the IMX_OPT_ENGINE environment variable.

Comparing the performances of CSOLNP, and NPSOL¶

Running the test suite of the package with both optimizers resulted in the following average running times:

NPSOL
real 3m58.2688s
user 3m56.4598s
sys 0m1.5264s

CSOLNP
real 4m13.9032s
user 4m11.8268s
sys  0m1.7012s

CSOLNP Documentation¶

Input¶

Output¶

Example¶

Restoring NPSOL¶

Comparing the performances of CSOLNP, and NPSOL¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

CSOLNP Documentation¶

Input¶

Output¶

Example¶

Restoring NPSOL¶

Comparing the performances of CSOLNP, and NPSOL¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation